An acceleration sensor is a common type of sensor that can measure the acceleration and tilt angle of objects, and is widely used in industries, healthcare, sports, and other fields. Acceleration sensors typically consist of sensing elements, signal processing circuits, and interface circuits, and can sense the acceleration of an object or detect changes in the motion state, converting these data into electrical signals for output.
Currently, the market offers two main types of acceleration sensors: analog sensors and digital sensors.
The characteristic of acceleration digital sensors is their ease of integration with digital systems. However, sometimes to achieve higher accuracy, lower noise, and to meet different dynamic response requirements, while also controlling costs, we tend to prefer analog output acceleration sensors.
Figure 1 shows the processing flow of the signal from a typical analog output accelerometer. Generally, to improve integration and reduce costs, the ADC sampling and digital filtering processing are integrated into the MCU or DSP internally.

Adding an anti-aliasing low-pass filter at the front end of the ADC (analog-to-digital converter) is a crucial design in the signal sampling system. According to the Nyquist sampling theorem, the ADC sampling frequency fs must be at least twice the highest frequency fmax of the signal (i.e., fs ≥ 2fmax) to accurately reproduce the original signal without distortion. If the input signal contains components with frequencies exceeding fs/2 (referred to as the Nyquist frequency), these high-frequency components will be "folded" into the low-frequency range, forming false signals (aliasing). Aliasing permanently contaminates the useful signal and cannot be eliminated through subsequent processing. The actual signal may contain noise or useless high-frequency components (such as electromagnetic interference, harmonics), which may exceed fs/2, and even if the input signal itself has a limited bandwidth, the sampling process of the ADC (especially discretization) will introduce quantization noise. The anti-aliasing low-pass filter can reduce the impact of high-frequency noise. The anti-aliasing low-pass filter is actually an RC (resistor-capacitor) low-pass filter, and its cutoff frequency fc is usually set slightly lower than fs/2 but slightly higher than the effective bandwidth of the signal (such as the bandwidth of an accelerometer of 100 Hz, fc is selected as 150 Hz), ensuring that only signals with frequencies below the Nyquist frequency pass through. If the ADC sampling clock frequency is 2 KHz, then the cutoff frequency fc should be set not higher than 1 KHz. The formula for calculating the cutoff frequency fc is fc = 1/(2π×R×C). Using the anti-aliasing low-pass filter to reduce background noise and thereby improve the resolution of the accelerometer. Generally, in the design, the bandwidth is limited to the lowest frequency required by the application to maximize the resolution and dynamic range of the accelerometer.
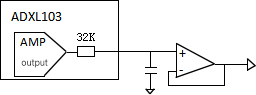
In practical use, if ADI's ADXL103 or ADXL203 is used, the internal low-pass filter is already integrated. The cutoff frequency (-3dB point) is determined by the external capacitor C connected to the output terminal, and only by connecting a capacitor in parallel to the output pin and forming a low-pass filter with the internal output resistor can the anti-aliasing and noise suppression functions be achieved. The actual application circuit is shown in Figure 2, and its corresponding fc = 5 µF/C.
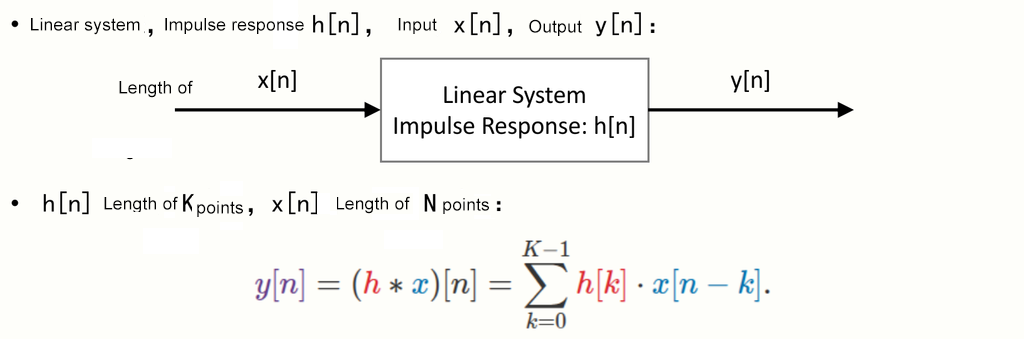
The analog signal passes through an anti-aliasing low-pass filter and is sent to the ADC module. Under the drive of the sampling clock, a continuous data stream is generated. At this time, the data inevitably still contains noise. To filter out the noise, digital filtering technology needs to be adopted to process the obtained data. Compared with analog filters, digital filters usually have more stable frequency responses, can precisely suppress out-of-band signals, have good repeatability, and can be implemented either in pure software or by using hardware acceleration of FIR (Finite Impulse Response) or IIR (Infinite Impulse Response) filters. Digital filtering can be either purely software-based or implemented using hardware acceleration of FIR or IIR.
Due to the high order of FIR filters, they consume more computing resources and are more suitable for running on DSP or high-performance MCUs. Their difference equation expression is shown in the following figure.
For a 120th-order low-pass FIR filter using a Kaiser window, the stopband attenuation usually reaches over 60dB. Compared to IIR filters, FIR filters have a wider transition band and larger group delay, and their real-time response is not as fast as IIR filters.
If the computing resources are limited on an embedded platform or to obtain a steeper transition band, IIR filters can also be used. Compared to FIR filters, IIR filters have higher computational efficiency (can achieve high performance with lower orders), have nonlinear phase changes, and are acceptable for accelerometers, but they may be unstable. The pole positions need to be carefully optimized. The general expression of the difference equation for IIR filters is as shown in the following figure.
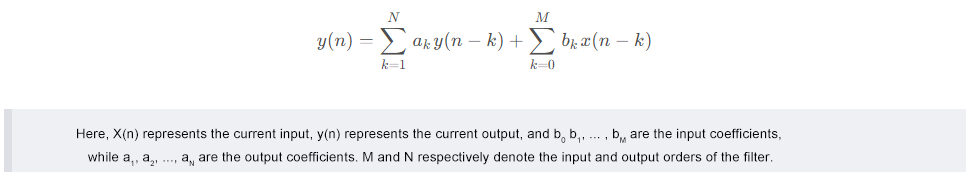
A 4th-order elliptic IIR low-pass digital filter usually can achieve a stopband attenuation of over 60dB when the passband ripple is 0.5dB.
Sometimes, in order to obtain a smooth output result, the output data within a certain window of the aforementioned filter is subjected to recursive average filtering to reduce the influence of noise. Given a signal sequence x[n] containing N samples, where n is the index of the sample (from 0 to N-1). Moving average filtering is performed by sliding a fixed-length window of length M over the signal sequence and calculating the average of the samples within the window. For each position k of the sliding window, the filtered output y[k] can be calculated using the following formula:
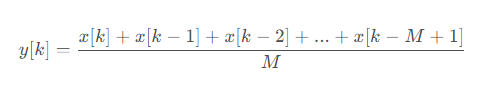
The size M of the sliding window determines the degree of smoothing. A larger window can more effectively smooth the signal, but it may result in a delayed response; a smaller window can respond to changes in the signal more quickly, but the smoothing effect may be poorer. Usually, when the ADC sampling clock is 2000Hz, M is set to 10.

Xml политика конфиденциальности блог Карта сайта
Авторское право
@ Микро-Мэджик Инк Все права защищены.
 ПОДДЕРЖИВАЕМАЯ СЕТЬ
ПОДДЕРЖИВАЕМАЯ СЕТЬ
